[ad_1]
The Birthday Paradox predicts that the probability of duplicates in random numbers is much higher than you’d think. For example, it predicts that, with a mere 23 random people, there’s a greater than 50% chance of two of them have the same birthday. By the Pigeonhole Principle, it takes 367 people for there to be a 100% chance of a duplicate, but the probability of a duplicate is extremely high even before that.
Here’s the probability distribution (from Wikipedia):
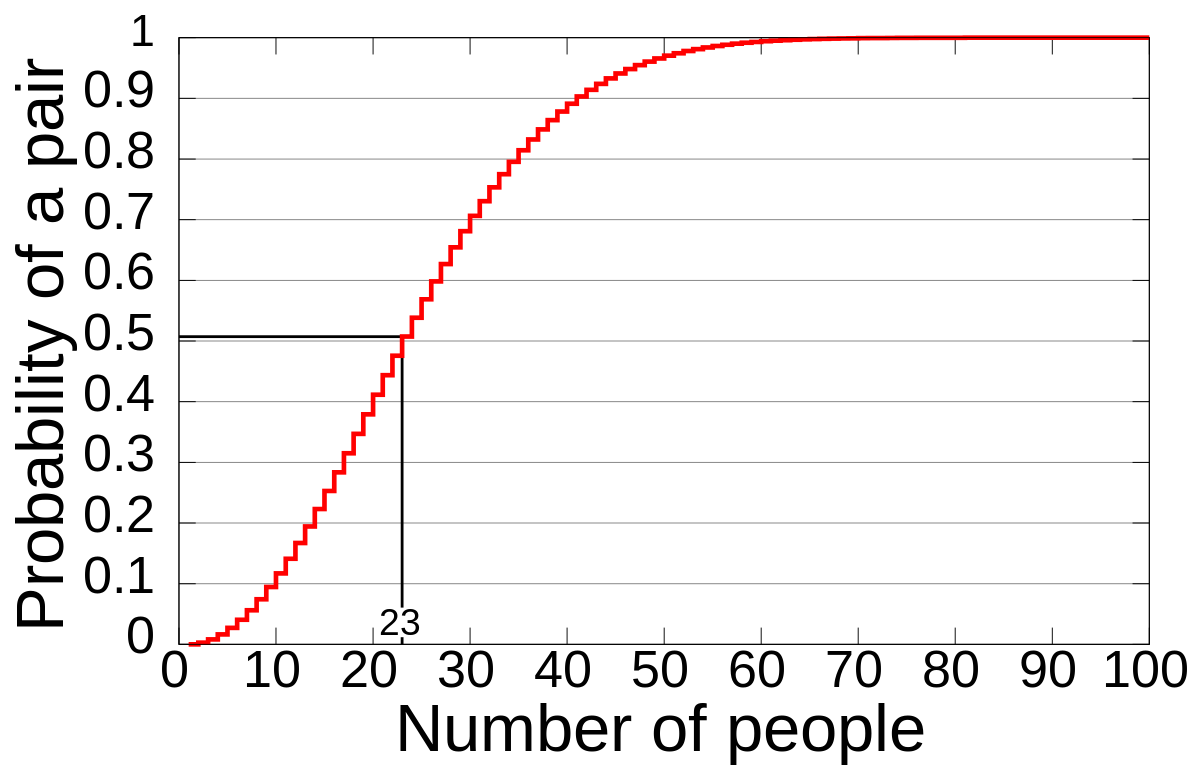
The rule of thumb to approximate the number of numbers you have to generate before the probability of duplicates reaches sqrt(2m * p(n)), where m is the number of possible random numbers and p(n) is the probability that you’re looking for. So, for example, if you’re generating random numbers in a 50-number range (e.g. if you pick a random number from 100 – 150), you’d only have to generate approximately sqrt((2 * 50) * 0.5) = 7.07 random numbers before the odds are just as good as not that you have a duplicate. If you generate 8 random numbers within a 50-number range, odds are better than not that’ll have a duplicate. (Note that this only works for p(n) values of up to 1/2).
In your case, there are 8 possible values for any particular random value (5, 6, 7, 8, 9, 10, 11, 12), so you only need to generate sqrt(8) = 2.83 numbers before there’s a probability of 50% that you’ll have a duplicate. In other words, the Birthday Paradox predicts you only need to generate approximately 3 numbers for the chances to be better than not that you’ll have a duplicate.
See also this Q&A.
One more point: beware the Gambler’s Fallacy, in which people assume that if you randomly generate, for example, a 10, odds are the next one won’t be a 10. Actually, given that you’re generating random numbers, the odds of any particular number is 1/8 regardless of what numbers came before. In other words, if you generate a 12, the probability of the next number being a 10 is 1/8. If you generate a 7, the odds of the next number being a 10 is 1/8. If you generate a 10, the probability of the next number being a 10 is still 1/8. Each number is an independent event (i.e. the numbers you’ve generated so far don’t influence the probability distribution of future numbers in the least).
TL;DR You need to generate much fewer numbers than you think you do before you’re likely to start getting duplicates – if you’re generating random numbers within a small range of numbers in particular (like you are) the number is particularly low.
[ad_2]
solved Random in Java often generating same value