[Solved] How to solve an equation with two variables in MATLAB [closed]

by


With your example equation, Rody’s answer provides an analytic solution.

In general, however, given an equation f(x,y)=0 it may not be possible to find an analytic solution. In that case I suggest:

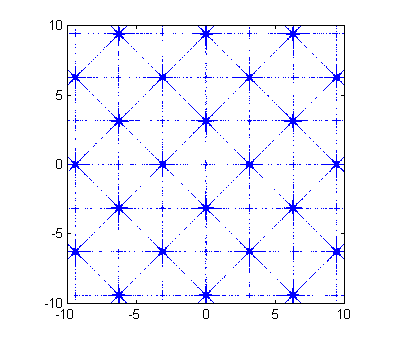
  1. Define a target x, y area and generate random samples within it.
  2. Compute z = abs(f(x,y)) at the sample points.

  3. Sort the values of z and define the approximate solution set as a given proportion of the lowest values.

    f = @(x,y) sin(x).*sin(2*y)+sin(y).*sin(2*x); %// your example function
N = 1e7; %// number of samples
proportion = 1e-2; %// choose to achieve thin lines in solution set
xmin = -10; xmax = 10; %// x limits of target area
ymin = -10; ymax = 10; %// y limits of target area

x = xmin+(xmax-xmin)*rand(1,N);
y = ymin+(ymax-ymin)*rand(1,N);
z = abs(f(x,y));
[zsort isort] = sort(z);
n = round(N*proportion);
plot(x(isort(1:n)),y(isort(1:n)),'b.','markersize',.1)
axis square

enter image description here

3

solved How to solve an equation with two variables in MATLAB [closed]