[Solved] Determine if data is related in R [closed]

by


Lets assume that

set.seed(44) 
deaths<- 10:1 + sample.int(3, 10, replace = T)

and

spent<- seq(100, 550, by = 50 )

The very first thing you want to do when you get your data is literally to look at it. This can be done relatively painlessly with 

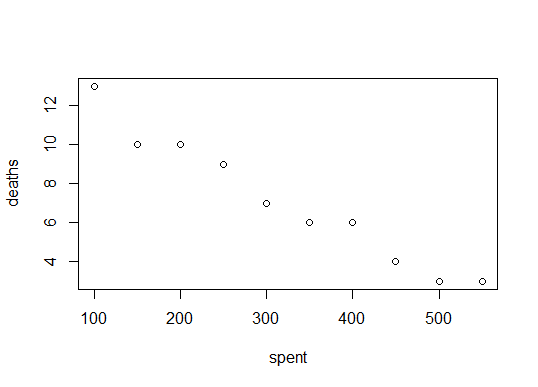
plot(spent, deaths)

which yields

enter image description here

So it looks like the more we spend, the less deaths there are. That makes sense. But how can we quantify that statement. Using cor() will give us the correlation between the two variables spent and deaths.

cor(spent, deaths)
# [1] -0.9809581

So it looks like they are very strong (and negatively correlated.) One other simple method (that is closely related to cor()) is to fit a linear model.

model<- lm(deaths~spent)

The summary() call yields a lot of useful information about the model you just fit, the interpretation of which is beyond the scope of this post, but can be readily found with some quick Googling.

summary(model) 

#Call:
#lm(formula = deaths ~ spent)

#Residuals:
# Min       1Q   Median       3Q      Max 
#-0.89697 -0.51515 -0.05758  0.46364  1.01818 

#Coefficients:
#            Estimate Std. Error t value Pr(>|t|)    
#(Intercept) 14.151515   0.539649   26.22 4.80e-09 ***
#spent       -0.021697   0.001519  -14.29 5.62e-07 ***
#---
#Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

#Residual standard error: 0.6898 on 8 degrees of freedom
#Multiple R-squared:  0.9623,   Adjusted R-squared:  0.9576 
#F-statistic: 204.1 on 1 and 8 DF,  p-value: 5.622e-07

solved Determine if data is related in R [closed]