[ad_1]
When in doubt, just break it down.
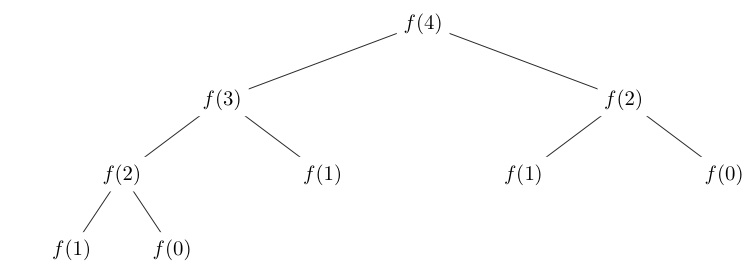
The tree flow is actually counter-intuitive to the actual control flow, but once you understand the sequence of calls, it becomes clearer. The thing to understand here is that you keep breaking down a larger computation to a sum of smaller computations, and you stop when you hit the base case (the if statements). Now you can carry out all the small computations, and combining the results of those small computations to form a bigger, larger result, until you have your final answer.
Every time a recursive call hits the base case, it will return either 1, or 0, depending on what case was hit. This value will be returned to the previous caller. To understand, consider:
f(1)3 + f(0)3Note here that the subscript represents the depth of the recursion call tree. The call is made by f(2)2. f(1)3 is computed first, and 1 is returned to f(2)2. f(0)3 is then computed, and 0 is returned to f(2)2. The two return values are summed, and the result is 1.
f(2)2 then returns 1 to whoever called it, which in this case happens to be f(3)1. f(3)1 called f(2)2 + f(1)2, meanwhile this other f(1)2 also returns 1 to f(3)1, who now adds that with the result of f(2)2, to form 2.
f(3)1 now passes 2 to f(4)0, its caller, which happened to call f(3)1 + f(2)1 … and so it goes.
An alternative way of looking at this is to start from the first function call that is actually made: f(4)0.
f(4)0 computes f(3)1 + f(2)1. But to compute f(3)1, it needs to know f(2)2 + f(1)2, and similarly, to compute f(2)1, it needs to know f(1)2 + f(0)2, and so on.
3
[ad_2]
solved Understanding recursion with the Fibonacci Series