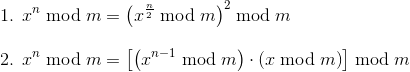[Solved] Modular Exponentiation (Power in Modular Arithmetic) [closed]

by


From the modulo laws on DAle’s linked Wikipedia page (on your previous question), we can obtain two formulas:

enter image description here

From the first formula it is clear that we can iteratively calculate the modulo for n from the result for n / 2. This is done by the lines

x = x * x;
x = x % m;

There are thus log n steps in the algorithm, because each time the exponent of x doubles. The step counting is done by n >>= 1 and while (n > 0), which counts log n steps.

Now, you may be wondering 1) why doesn’t this part set the value of res, and 2) what is the purpose of these lines

if(n & 1){
   res = res * x;
   res = res % m;
}

This is necessary as at certain points in the iteration, be it the start or the end, the value of n may be odd. We can’t just ignore it and keep using formula 1, because that means we would skip a power of x! (Integer division rounds down, so e.g. 5 >> 1 = 2, and we would have x^4 instead of x^5). This if statement handles the case when n is odd, i.e. n % 2 = n & 1 = 1. It simply uses formula 2 above to “add” a single power of x to the result.

solved Modular Exponentiation (Power in Modular Arithmetic) [closed]